Heute gibt es ein wenig Augenschmaus, den man mathematisch, aber auch, wie das Bild links zeigt, kulinarisch fortsetzen kann. Es gibt einige mathematische Verfahren, mit denen man Muster erzeugt, welche natürlichen Strukturen wie Landschaften oder Pflanzen erstaunlich ähnlich sehen. Zwei davon möchte ich kurz vorstellen: Fibonacci-Zahlen und Fraktale. Die Mathematik bleibt dabei hinter den Links versteckt und der Fokus liegt auf der Optik und ein wenig philosophisch-biologischer Spekulation.
Der Romanesco-Broccoli, der im Bild unten zu sehen ist, beinhaltet Merkmale beider mathematischer Verfahren: Seine Gesamtstruktur ist fraktal und die Spiralen folgen einer Fibonacci-Folge. Die Mathematik hinter beiden ist eigentlich relativ schlicht, aber trotzdem taucht die Frage auf, wo dieser Kohlkopf Mathematik gelernt hat?
Der Bauplan eines solchen Gewächses ist natürlich in seinen Genen gespeichert. Diesen Bauplan kann man sich freilich nicht wie den eines Gebäudes vorstellen, denn es gibt keinen Architekten oder Handwerker, der mit dem Gesamtbild des Organismus vor Augen mit dem Bau beginnt. Statt dessen muss der Bauplan so hinterlegt sein, dass darin Anweisungen für die einzelnen Zellen der Pflanze enthalten sind: Diese müssen wissen, wie sie sich zu teilen und weiter zu wachsen haben. Dazu muss im Genom eine einfache Handlungsvorschrift, also ein Algorithmus, abgelegt sein, dem die einzelnen Zellen folgen. Aus den lokalen Aktionen aller Zellen entspringt dann die Gesamtform der Pflanze.
Eine solche einfache Handlungsvorschrift führt zu geometrischen Mustern. Wenn sie geschickt gewählt ist, dann können diese Muster komplexe Strukturen bilden und durch kleine Veränderung ihrer Parameter Abwandlungen der resultierenden Form erzeugen. Mit anderen Worten: Einen mathematischen Algorithmus auf diese Weise in den Genen zu hinterlegen, ist eine für die Evolution sehr effiziente Form zur Speicherung und Weiterentwicklung des Bauplans eines Organismus.
Eine Nebenbemerkung: Mathematik begegnet uns nicht nur in den Bauplänen lebender Organismen, sondern auch in der unbelebten Natur. Wer ein Einführungsbuch zur Physik aufschlägt, kann sich wundern, wie weit man mit der Beschreibung der Natur gelangen kann durch Nutzung so trivialer mathematischer Mittel wie Grundrechenarten, Wurzeln und Potenzen, Logarithmen und simplen Winkelfunktionen. Ist dies selbstverständlich oder sagt uns dies etwas über das tiefere Wesen der Natur? Die Frage ist nicht esoterisch gemeint und Fragen der Art „Ist Gott ist ein Mathematiker?“ könnten – milde gesagt – leicht verfrüht sein, aber das Hangeln an diesem spekulativen Zweig überlasse ich heute dem Leser.
Kommen wir zur Fibonacci-Folge, die nach dem italienischen Mathematiker Leonardo Fibonacci benannt ist. Dieser lebte um 1200 und war der bedeutenste Mathematiker seiner Zeit mit einer interessanten Lebensgeschichte. Die Fibonacci-Folge funktioniert ganz schlicht: Ich schreibe eine Reihe von Zahlen hintereinander, in dem ich immer die letzten beiden Zahlen nehme und die nächste durch die Addition der beiden vorhergehenden erzeuge. Weil ich einen Startpunkt benötige, beginne ich einfacherweise mit zwei Einsen und erhalte 1, 1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 usw.
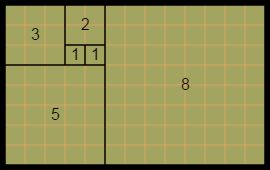
Dies kann man bereits für die Konstruktion einer einfachen geometrischen Form verwenden. Ein erstes Quadrat mit der Kantenlänge 1 wird gemalt, daneben ein zweites. Das nächste Quadrat hat die Kantenlänge der beiden vorhergehenden. Das Ergebnis sieht nach ein paar Schritten noch nicht sehr aufregend sondern so aus:
In dieses einfache Muster kann man nun aber eine Kurve einpassen, die interessante Eigenschaften hat. Ihr Radius verändert sich schrittweise in einem Verhältnis, welches sehr nahe am goldenen Schnitt ist. Dies ist eine Proportion, die seit der Antike als die ästhetisch ideale gilt, wenn es darum geht, Größenverhältnisse festzulegen. Die Spirale, die man in die oben stehende Form einpassen kann, nennt man daher auch goldene Spirale.
Das sind natürlich alles trockene abstrakte Worte. Wie der Schritt von den oben stehenden Rechtecken zu den goldenen Spiralen und von dort zu Mustern in der Natur aussehen kann, hat der spanischen Künstler Cristóbal Vila in einem wunderschönen Video illustriert: Er nannte es „Nature by Numbers“ und erläutert auf seiner Webseite auch die Mathematik dahinter. Also: Licht dimmen, zurücklehnen und genießen …
Kommen wir zum zweiten Thema: Den Fraktalen. Dies sind geometrische Strukturen, die keine ganzzahligen Dimensionen haben: Eine Linie ist eindimensional, eine „normale“ euklidische Fläche zweidimensional und ein Würfel ist dreidimensional. Fraktale haben Dimensionen, die dazwischen liegen. Wem das merkwürdig vorkommt, der ist damit nicht allein, wird aber trotzdem auf Wikipedia verwiesen: Ich will hier keine Leser mit Mathematik vergraulen !
Solche Fraktale haben verblüffende geometrische Eigenschaften: Die Muster, die durch sie beschrieben werden, weisen eine Eigenschaft auf, die man Selbstähnlichkeit nennt. Damit meint man, dass Teile des Musters genauso aussehen wie das Gesamtmuster. Dies ist so wie bei einem Foto, bei dem man nicht genau weiß, ob darauf eine ganze Bergflanke zu sehen ist oder nur ein kleiner Stein: Die große Struktur sieht genauso aus wie ihre Teile.
Das hat einen interessanten Nebeneffekt: Die Frage, wie groß die Oberfläche des Felsen ist, kann nicht leicht beantwortet werden. Ein erster Antwortansatz könnte sein, auf den Felsen eine glatte Fläche zu legen: Er ist 100 Meter hoch und 100 Meter breit, also ist die Fläche 100 Quadratmeter. Legt man dann ein Tuch dieser Größe auf den Felsen und drückt es in die Vertiefungen, so stellt man fest, dass die Oberfläche wesentlich größer ist. Bei einer selbstähnlichen Struktur kann man beliebig nah heranfahren: Es tun sich immer wieder neue Vertiefungen und Verzweigungen auf, die genauso aussehen wie die bei gröberen Vergrößerungen. Die Oberfläche ist „gebrochen“ bzw. „rau“. Mehr will ich zur Theorie nicht sagen, sondern lieber auf die Ästhetik übergehen: Auf den Begriff der „Rauheit“ kommen wir dabei gleich noch einmal zurück.
Beginnen möchte ich mit einer speziellen Form von Fraktalen, die Aristid Lindenmayer 1968 vorstellte: Die L-Systeme. Sie können vor allem eingesetzt werden, um Pflanzenstrukturen mathematisch zu erzeugen: Das Bild zeigt ein paar Beispiele, welche durch leichte Modifikation der Parameter zu Stande kommen.
Der Begriff der Fraktale ist untrennbar mit dem Namen Benoit Mandelbrot verbunden, nach dem die Mandelbrot-Menge benannt wurde; manche(r) kennt dazu vielleicht auch die Bezeichnung „Apfelmännchen“. Zur Popularität seiner Überlegungen trug das Aufkommen von leistungsfähigen Computern entscheidend bei, denn plötzlich konnten diese Strukturen einfach visualisiert werden. Man erkannte ihre Schönheit und entdeckte Anwendungsmöglichkeiten im Bereich der Modellierung realer Objekte wie Landschaften und anderen natürlichen Strukturen, aber auch in weniger visuellen Bereichen wie der Verschlüsselung und Datenkompression.
Im Jahr 1986 erschien dazu der Klassiker „Beauty of Fractals“ von Peitgen und Richter, der mich selbst auch dazu verführte, eigene kleine Programme zu schreiben. Solche Programme füllten damals in quälender Langsamkeit die Bildschirme der noch leistungsschwachen Heimrechner Pixel für Pixel. Heute gibt es Stapel an Büchern zu dem Thema und bequeme frei erhältliche Software oder auch gleich fertige Bildergalerien. Von den Büchern möchte ich nur eines empfehlen, welches sich nicht nur auf Fraktale beschränkt: „Mathematik sehen und verstehen“ von Dörte Haftendorn; auf Amazon kann man das Kapitel über Fraktale und Lindenmayer-Systeme ab Seite 89 im Preview anschauen.
Beispiele für „fractal art“ mit Fraktalbildgalerien findet man im Internet zuhauf, z.B. von Fractal Recursions, Alice Kelley oder die Fractal Art Gallery, in der auch Softwarehinweise zu finden sind, mit denen man Fraktale auf eigene Faust erkunden kann. Auf Youtube findet man ebenfalls zahlreiche Videos zu Fraktalen, als Beispiel verlinke ich einen „deep dive„, in dem man gut erkennen kann, wie die Ausgangsform des Apfelmännchens in den Tiefen der Struktur immer wieder erscheint.
Der Vater dieser Mathematik, Benoit Mandelbrot, starb leider im Oktober 2010. Einer seiner letzten großen öffentlichen Auftritte war ein paar Monate vorher auf einer TED-Konferenz, in der er erläuterte, was es mit der „Rauheit“ von Fraktalen auf sich hat. Ein beeindruckender Mann mit einem beeindruckenden Leben: Ein echter Querdenker, der wichtige Inspirationen gesetzt hat und an dem man sich nicht nur beim Essen von Romanesco-Broccoli erinnern sollte. Viel Spaß beim Anschauen seiner Präsentation.